<0 hay="" libres="" no="">Errara corregida el 16/07/24 en la línea 3050
Los arboles son las estructuras mas usadas para almacenar datos, ya que permiten un muy rápido acceso a ellos. La estructura en sencilla, un registro se divide en dos partes, una con los datos que se necesitan guardar y otro con enlaces a los elementos hijos, que será un número mayor o igual a dos.
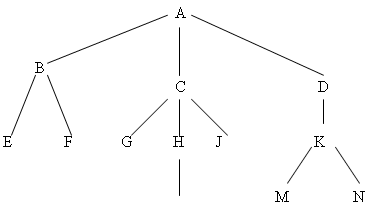 |
| Ejemplo de arbol (Fuente: Monografias.com) |
Si el número máximo de hijos es dos se denominan árboles binarios, y son los mas usados en programación en general, reservando los árboles de mas ramas para uso en ficheros indexados habitualmente. No voy a explicar mucho mas, hay suficiente información en la Web sobre arboles y su manejo.
Existe un tipo especial de árbol binario, en el que en cada nodo de cada rama, los valores de los elementos que cuelgan del nodo izquierdo son todos menores al valor del propio nodo, y los elementos que cuelgan del nodo derecho son todos valores mayores al del propio nodo, de forma que si recorremos el árbol primero la rama izquierda, luego el nodo, y luego la rama derecha, obtenemos una lista de elementos ordenados en orden creciente. Si la recorremos primero la rama derecha, luego el nodo y después la rama izquierda obtenemos la lista ordenada en forma decreciente. Este tipo de árboles se llaman "Árbol Binario de Búsqueda", y es lo que voy a implementar, ya que estamos hablando de algoritmos de ordenación.
Voy a usar tres arreglos para almacenar los datos, en uno me guardo los datos del registro (en este caso será una lista de números, pero puede ser cambiado de manera sencilla a una lista de cadenas por ejemplo), otro arreglo numérico con los enlaces a los punteros de la rama izquierda, y un tercer arreglo con los enlaces a la rama derecha. Estos dos arreglos podrían ser uno solo, pero creo que así está un poco mas claro.
Usaré el arreglo de enlaces a nodos izquierdos para almacenar la lista de elementos libres, pero por que sea mas visual haré lo mismo con los derechos. Esto lo cambiaré mas adelante por algo un poco mejor, ya lo veremos. El manejo de los árboles requiere muchos procedimientos recursivos, aunque usaré iterativos cuando sea posible para que se vean varias técnicas de manejo.
Uso una variable para almacenar el nivel máximo de profundidad del árbol, no tiene uso mas que para enseñarlo en pantalla, pero me permite que se vea algo que deseo demostrar luego. No me voy a complicar mucho cuando compacto el árbol, ya que esta parte la voy a cambiar luego, solo lo pongo de momento para que se vea.
2000 REMark -------------------------------------------------------------- 2010 REMark -- ESTRUCTURAS DE DATOS -- 2020 REMark -- Modulo....: Arbol binario -- 2030 REMark -- Objetivo..: Arbol binario usando un arreglo de valores -- 2040 REMark -- numericos y dos para los punteros -- 2050 REMark -- Autor.....: javu61, 12/2016 -- 2060 REMark -- Procesos..: -- 2070 REMark -- ARBOL_CREAR -- Crear el arbol -- 2080 REMark -- ARBOL_NUEVO(tam) -- Crea el arbol con un tama‰o -- 2090 REMark -- b=ARBOL_LEN -- Nro de elementos del arbol -- 2100 REMark -- b=ARBOL_NIVELES -- Nro de niveles del arbol -- 2110 REMark -- b=ARBOL_BUSCAR(n)-- Busca un elemento en el arbol -- 2120 REMark -- ARBOL_ADD(dato) -- Introduce un dato en el arbol -- 2130 REMark -- ARBOL_DELETE(n) -- Borra el elemento n del arbol -- 2140 REMark -- v$=ARBOL_VER$ -- Muestra los elementos del arbol -- 2150 REMark -- ARBOL_CAMBIA(tam)-- Cambia el tama‰o del arbol -- 2160 REMark -- Procesos de uso interno: -- 2170 REMark -- ARBOL_INIT -- Inicializa una arbol -- 2180 REMark -- b=ARBOL_EL_LIBRE -- Retorna elemento libre -- 2190 REMark -- n=ARBOL_NIVELES -- Retorna nro de niveles del arbol -- 2200 REMark -- Elementos.: Se usan los siguientes elementos globales -- 2210 REMark -- A_TAM -- Tama‰o del arreglo -- 2220 REMark -- A_FACTOR -- Factor de crecimiento -- 2230 REMark -- ArrArbol(tam) -- Elementos del arbol -- 2240 REMark -- ArrIzq(tam) -- Puntero al elemento izquierdo -- 2250 REMark -- ArrDer(tam) -- Puntero al elemento derecho -- 2260 REMark -- P_NULO -- Puntero nulo -- 2270 REMark -- P_VACIO -- Puntero vacio -- 2280 REMark -- A_RAIZ -- Puntero al nodo raiz -- 2290 REMark -- A_NRO -- Nro de elementos del arbol -- 2300 REMark -- A_NIVELES -- Nro de niveles del arbol -- 2310 REMark -------------------------------------------------------------- 2320 : 2330 : 2340 REMark -------------------------------------------------------------- 2350 REMark -- ARBOL_CREAR -- Crea el arbol -- 2360 REMark -------------------------------------------------------------- 2370 DEFine PROCedure ARBOL_CREAR 2380 REMark Espacio para 10 elementos, crece minimo 5 2390 ARBOL_NUEVO 9,5 2400 END DEFine 2410 : 2420 REMark -------------------------------------------------------------- 2430 REMark -- ARBOL_NUEVO(tam,fac) -- Crea el arbol con un tama‰o y un -- 2440 REMark -- factor de crecimiento -- 2450 REMark -------------------------------------------------------------- 2460 DEFine PROCedure ARBOL_NUEVO(tam,fac) 2470 LOCal i 2480 : 2490 LET P_NULO = -1 : REMark Puntero nulo 2500 LET P_VACIO = -2 : REMark Puntero vacio 2510 LET A_RAIZ = P_NULO : REMark Puntero al nodo raiz 2520 LET A_NIVELES= 0 : REMark Nro de niveles del arbol 2530 LET A_NRO = 0 : REMark Nro de elementos del arbol 2540 LET A_TAM = tam : REMark Tama‰o del arreglo 2550 LET A_FACTOR = fac : REMark Factor de crecimiento 2560 DIM ArrIzq(tam) : REMark Punteros al elemento izquierdo 2570 DIM ArrDer(tam) : REMark Punteros al elemento derecho 2580 DIM ArrArbol(tam) : REMark Elementos del arbol 2590 : 2600 REMark Inicializa arbol de elementos libres 2610 FOR i=0 TO A_TAM : ArrIzq(i) = P_VACIO : ArrDer(i) = P_VACIO 2620 END DEFine 2630 : 2640 REMark -------------------------------------------------------------- 2650 REMark -- b = ARBOL_LEN -- Retorna el nro de elementos del arbol -- 2660 REMark -- RETORNA: 0 si vacio, >0 = nro de elementos -- 2670 REMark -------------------------------------------------------------- 2680 DEFine FuNction ARBOL_LEN 2690 RETurn A_NRO 2700 END DEFine 2710 : 2720 REMark -------------------------------------------------------------- 2730 REMark -- b = ARBOL_NIVELES -- Retorna el nro de niveles del arbol -- 2740 REMark -- RETORNA: 0 si vacio, >0 = nro de elementos -- 2750 REMark -------------------------------------------------------------- 2760 DEFine FuNction ARBOL_NIVELES 2770 RETurn A_NIVELES 2780 END DEFine 2790 : 2800 REMark -------------------------------------------------------------- 2810 REMark -- b = ARBOL_EL_LIBRE -- Retorna elemento libre del arbol -- 2820 REMark -- RETORNA: <0 hay="" libres="" no="">=0 nro del elemento -- 2830 REMark -------------------------------------------------------------- 2840 DEFine FuNction ARBOL_EL_LIBRE 2850 LOCal i 2860 : 2870 FOR i=0 TO A_TAM 2880 IF ArrIzq(i) = P_VACIO THEN RETurn i 2890 END FOR i 2900 RETurn P_NULO 2910 END DEFine 2920 : 2930 REMark -------------------------------------------------------------- 2940 REMark -- b = ARBOL_BUSCAR(valor) -- Busca un elemento en el arbol -- 2950 REMark -- RETORNA: nro del elemento o NULO si no encontrado -- 2960 REMark -------------------------------------------------------------- 2970 DEFine FuNction ARBOL_BUSCAR(valor) 2980 LOCal nro,repetir 2990 : 3000 nro = A_RAIZ 3010 REPeat repetir 3020 IF nro = P_NULO THEN EXIT repetir 3030 IF ArrArbol(nro) = valor THEN EXIT repetir 3040 IF ArrArbol(nro) < valor THEN 3050 nro = ArrIzq(nro) : REMark errara corregida 16/07/24 3060 ELSE 3070 nro = ArrDer(nro) 3080 END IF 3090 END REPeat repetir 3100 RETurn nro 3110 END DEFine 3120 : 3130 : 3140 REMark -------------------------------------------------------------- 3150 REMark -- ARBOL_ADD(dato) -- Introduce un dato en el arbol, si -- 3160 REMark -- esta llena crece al doble -- 3170 REMark -------------------------------------------------------------- 3180 DEFine PROCedure ARBOL_ADD(dato) 3190 LOCal repetir,nro,pos,nivel 3200 : 3210 REMark Busco nodo libre, crece si hace falta y ubico el elemento 3220 REPeat repetir 3230 nro = ARBOL_EL_LIBRE 3240 IF nro <> P_NULO THEN EXIT repetir 3250 ARBOL_CAMBIA(A_TAM*2) 3260 END REPeat repetir 3270 ArrArbol(nro) = dato 3280 ArrIzq(nro) = P_NULO 3290 ArrDer(nro) = P_NULO 3300 nivel = 1 3310 : 3320 REMark Si es el primer nodo, lo ubico en la raiz 3330 IF A_RAIZ = P_NULO THEN 3340 A_RAIZ = nro 3350 ELSE 3360 REMark Si no es el primero, buscamos su posicion recorriendo 3370 pos = A_RAIZ 3380 REPeat repetir 3390 nivel = nivel + 1 3400 REMark Si es menor o igual pasamos a la izquierda 3410 IF (ArrArbol(pos) > dato) THEN 3420 IF (ArrIzq(pos)=P_NULO) THEN 3430 ArrIzq(pos) = nro 3440 EXIT repetir 3450 END IF 3460 pos = ArrIzq(pos) 3470 ELSE 3480 : 3490 REMark Si es mayor pasamos a la derecha 3500 IF (ArrDer(pos)=P_NULO) THEN 3510 ArrDer(pos) = nro 3520 EXIT repetir 3530 END IF 3540 pos = ArrDer(pos) 3550 END IF 3560 END REPeat repetir 3570 END IF 3580 : 3590 REMark Sumo un elemento al arbol y miro el nivel 3600 A_NRO = A_NRO + 1 3610 IF nivel > A_NIVELES THEN A_NIVELES = nivel 3620 : 3630 END DEFine 3640 : 3650 REMark -------------------------------------------------------------- 3660 REMark -- v$ = ARBOL_VER$ -- Muestra el arbol -- 3670 REMark -- RETORNA: Lista de elementos del arbol -- 3680 REMark -------------------------------------------------------------- 3690 DEFine FuNction ARBOL_VER$(hastanivel) 3700 LOCal lista$ 3710 : 3720 IF ARBOL_LEN = 0 THEN 3730 PRINT "Error: Arbol vacio" 3740 STOP 3750 END IF 3760 : 3770 lista$="" 3780 inorden A_RAIZ,hastanivel,lista$,1 3790 RETurn lista$ 3800 END DEFine 3810 : 3820 DEFine PROCedure inorden(nodo,nivel,cadena$,actual) 3830 IF nodo <> P_NULO THEN 3840 inorden ArrIzq(nodo),nivel,cadena$,actual+1 3850 IF (nivel < 1) OR (nivel = actual) THEN 3860 IF LEN(cadena$) <> 0 THEN cadena$ = cadena$ & "," 3870 cadena$ = cadena$ & "[" & actual & "]" & ArrArbol(nodo) 3880 END IF 3890 inorden ArrDer(nodo),nivel,cadena$,actual+1 3900 END IF 3910 END DEFine 3920 : 3930 REMark -------------------------------------------------------------- 3940 REMark -- ARBOL_DELETE(valor) -- Borra un elemento del arbol -- 3950 REMark -------------------------------------------------------------- 3960 DEFine PROCedure ARBOL_DELETE(valor) 3970 LOCal nodo,padre,repetir 3980 : 3990 nodo = A_RAIZ 4000 padre = P_NULO 4010 REPeat repetir 4020 IF nodo = P_NULO THEN EXIT repetir 4030 IF ArrArbol(nodo) = valor THEN EXIT repetir 4040 padre = nodo 4050 IF ArrArbol(nodo) < valor THEN nodo = ArrDer(nodo) 4060 IF ArrArbol(nodo) > valor THEN nodo = ArrDer(nodo) 4070 END REPeat repetir 4080 : 4090 IF (nodo = P_NULO) THEN 4100 PRINT "ERROR: Intenta eliminar un elemento que no existe" 4110 STOP 4120 END IF 4130 : 4140 ARBOL_BORRAR_NODO nodo,padre : REMark Borrar el nodo 4150 A_NRO = A_NRO - 1 : REMark reducir elementos del arbol 4160 A_NIVELES = ARBOL_MAX_NIVEL : REMark Recalcula niveles 4170 END DEFine 4180 : 4190 REMark -------------------------------------------------------------- 4200 : 4210 DEFine PROCedure ARBOL_BORRAR_NODO(nodo,padre) 4220 LOCal nuevo 4230 : 4240 :: ArrArbol(nodo) = 0 4250 : 4260 REMark Este elemento sera el que reemplace en el padre 4270 nuevo = P_NULO 4280 : 4290 REMark Si no tiene hijos, se desapunta el padre 4300 IF (ArrIzq(nodo)=P_NULO) AND (ArrDer(nodo)=P_NULO) THEN 4310 nuevo = P_NULO 4320 END IF 4330 : 4340 REMark Solo tiene un hijo, se pasa al padre 4350 IF (ArrIzq(nodo)=P_NULO) AND (ArrDer(nodo)<>P_NULO) THEN 4360 nuevo = ArrDer(nodo) 4370 END IF 4380 IF (ArrIzq(nodo)<>P_NULO) AND (ArrDer(nodo)=P_NULO) THEN 4390 nuevo = ArrIzq(nodo) 4400 END IF 4410 : 4420 REMark Tiene dos hijos, pasa al padre el derecho y lo borro 4430 IF (ArrIzq(nodo)<>P_NULO) AND (ArrDer(nodo)<>P_NULO) THEN 4440 nuevo = ArrDer(nodo) 4450 ARBOL_BORRAR_NODO ArrDer(nodo),nodo 4460 END IF 4470 : 4480 REMark Ahora apunto el padre de forma adecuada 4490 IF padre = P_NULO THEN 4500 A_RAIZ = nuevo 4510 ELSE 4520 IF ArrIzq(padre) = nodo THEN ArrIzq(padre) = nuevo 4530 IF ArrDer(padre) = nodo THEN ArrDer(padre) = nuevo 4540 END IF 4550 ArrIzq(nodo) = P_VACIO 4560 ArrDer(nodo) = P_VACIO 4570 END DEFine 4580 : 4590 REMark -------------------------------------------------------------- 4600 REMark -- ARBOL_CAMBIA -- Cambia el tama‰o del arbol -- 4610 REMark -------------------------------------------------------------- 4620 DEFine PROCedure ARBOL_CAMBIA(tam) 4630 LOCal tEle(A_TAM),tIzq(A_TAM),tDer(A_TAM),tTam,tRaiz,tNro,m1,m2,i 4640 : 4650 REMark Guardo el arbol en el auxiliar de forma compacta 4660 tRaiz = A_RAIZ 4670 tNro = A_NRO 4680 tTam = A_TAM 4690 m1 = 0 : REMark Ultimo elemento libre de la lista 4700 FOR i=A_TAM TO 0 STEP -1 4710 IF (m1 = 0) AND (tEle(i) <> P_VACIO) THEN 4720 m1 = i + 1 4730 END IF 4740 tEle(i)=ArrArbol(i) 4750 tIzq(i)=ArrIzq(i) 4760 tDer(i)=ArrDer(i) 4770 END FOR i 4780 : 4790 REMark calculo tama‰os m“nimos 4800 m2 = A_NRO + A_FACTOR 4810 IF tam < m2 THEN tam = m2 4820 IF tam < A_FACTOR THEN tam = tam + A_FACTOR 4830 IF tam < m1 THEN tam = m1 + A_FACTOR 4840 : 4850 REMark Creo el nuevo arbol y lo relleno 4860 ARBOL_NUEVO tam,A_FACTOR 4870 : 4880 A_RAIZ = tRaiz 4890 A_NRO = tNro 4900 FOR i=0 TO m1-1 4910 ArrArbol(i) = tEle(i) 4920 ArrIzq(i) = tIzq(i) 4930 ArrDer(i) = tDer(i) 4940 END FOR i 4950 END DEFine 4960 : 4970 : 4980 REMark -------------------------------------------------------------- 4990 REMark -- n = ARBOL_NIVELES -- Retorna el nro de niveles del arbol -- 5000 REMark -- RETORNA: Nivel maximo del arbol -- 5010 REMark -------------------------------------------------------------- 5020 DEFine FuNction ARBOL_MAX_NIVEL 5030 RETurn nivel_inorden(A_RAIZ, 0) 5040 END DEFine 5050 : 5060 DEFine FuNction nivel_inorden(nodo,actual) 5070 LOCal n1,n2 5080 : 5090 IF nodo = P_NULO THEN 5100 RETurn actual 5110 ELSE 5120 n1 = nivel_inorden(ArrIzq(nodo),actual+1) 5130 n2 = nivel_inorden(ArrDer(nodo),actual+1) 5140 IF (n1 > n2) THEN RETurn n1 : ELSE RETurn n2 5150 END IF 5160 END DEFine
Para poder verificar que el árbol funciona uso un pequeño programa de pruebas, en el se ve siempre el árbol y sus enlaces izquierdo y derecho, los punteros nulos, los elementos libres, etc. Tras cada prueba se presenta el árbol y la lista de elementos ordenados que se obtiene del mismo.
100 REMark ----------------------------------------
110 REMark -- Carga --
120 REMark ----------------------------------------
130 MODE 4: PAPER 0 : CLS
140 INPUT "Cual prefiere (1)=Simple",t$
150 IF t$<>"1" THEN GO TO 200
160 n$="mdv1_ed_arbol_arreglo" & t$
170 PRINT "Cargando ";n$
180 MERGE n$
190 REMark ----------------------------------------
200 REMark -- Rutinas de pruebas --
210 REMark ----------------------------------------
220 MODE 4: PAPER 0 : CLS : LET No=0 : LET Si=1
230 p2$=""
240 t1=DATE
250 :
260 PRINT "Creacion del arbol"
270 crear : ver : PRINT
280 :
290 PRINT "PRUEBA 1: Introduce elementos en orden, inversos y aleatorios"
300 crear : FOR i=1 TO 5 : mete(i) : END FOR i : verarbol
310 crear : FOR i=5 TO 1 STEP -1 : mete(i) : END FOR i : verarbol
320 crear : FOR i=1 TO 10 : mete(RND(1 TO 9)): END FOR i : verarbol
330 :
340 PRINT "PRUEBA 2: Introduce 9, elimina 5, introduce 3, elimina 4"
350 crear
360 FOR i=1 TO 9 : mete(i)
370 FOR i=1 TO 5 : borra(i)
380 FOR i=10 TO 12 : mete(i)
390 FOR i=9 TO 11 : borra(i)
400 verarbol
410 :
420 PRINT "PRUEBA 3: Introduce 9, Extrae 2, introduce 10 y reduce"
430 crear
440 FOR i=1 TO 9 : mete(i)
450 FOR i=1 TO 2 : borra(i)
460 FOR i=10 TO 19 : mete(i)
470 verarbol
480 PRINT "CM "; : ARBOL_CAMBIA 0 : ver : verarbol
490 :
500 PRINT "PRUEBA 4: Buscar algunos elementos"
510 crear
520 FOR i=1 TO 9 : mete(i)
530 FOR i= 0 TO 13 STEP 3
540 PRINT "BUSCO ";i;" = ";ARBOL_BUSCAR(i)
550 END FOR i
560 PRINT
570 :
580 PRINT "PRUEBA 5: Extrae elementos hasta error por vacia"
590 FOR i=1 TO ARBOL_LEN : borra(i)
600 t2 = DATE : PRINT "Tarda ";t2-t1;" segundos"
610 borra(0)
620 STOP
630 :
640 :
650 DEFine PROCedure crear
660 ARBOL_CREAR
670 END DEFine
680 :
690 DEFine PROCedure mete(a)
700 PRINT "EN ";a;":";
710 ARBOL_ADD(a)
720 ver
730 END DEFine
740 :
750 DEFine PROCedure borra(a)
760 PRINT "BO ";!a;"(";ARBOL_BUSCAR(a);"):";
770 ARBOL_DELETE(a) : ver
780 END DEFine
790 :
800 DEFine PROCedure verarbol
810 PRINT "ARBOL: ";ARBOL_VER$(0) : PRINT
820 END DEFine
830 :
840 DEFine PROCedure ver
850 LOCal xx
860 :
870 PRINT "[";ARBOL_LEN;"x";ARBOL_NIVELES;"]";
880 IF A_RAIZ=P_NULO THEN PRINT "*"; : ELSE PRINT A_RAIZ;":";
890 FOR xx=0 TO A_TAM
900 PRINT !"(";xx;")";ArrArbol(xx);
910 IF ArrIzq(xx)=-1 THEN PRINT "*";
920 IF ArrIzq(xx)=-2 THEN PRINT "v";
930 IF ArrIzq(xx)>0 THEN PRINT ArrIzq(xx);
940 IF ArrDer(xx)=-1 THEN PRINT "*";
950 IF ArrDer(xx)=-2 THEN PRINT "v";
960 IF ArrDer(xx)>0 THEN PRINT ArrDer(xx);
970 END FOR xx
980 PRINT
990 END DEFine
Cuando ejecutéis las pruebas os daréis cuenta de que si introduzco los elementos de forma ordenada todos van a parar siempre a la rama derecha, quedando la izquierda vacía, por lo que tenemos una lista en lugar de un árbol. Cuando los introduzco de forma aleatoria se van llenando las ramas izquierda y derecha mas o menos a la par. Esto nos indica que un árbol binario de búsqueda solo será eficiente si los elemento se introducen al azar y producen un árbol en el que las ramas sean todas mas o menos del mismo tamaño, pues sin ese equilibrio pierde mucha efectividad en altas y bajas, pero lo que es peor, hace mas lentas las búsquedas, siendo nuestro objetivo que estas sean lo mas eficientes posibles. En la siguiente entrada montaremos arboles binarios de búsqueda equilibrados mediante las técnicas de rotación simple y doble, produciendo árboles AVR.
Como siempre aquí todo lo desarrollado sobre estructuras de datos hasta el momento, la parte de ordenación no ha variado.
Fantástica esta colección de artículos sobre algoritmos con SuperBasic. Da gusto "leer" ese código fuente Basic.
ResponderEliminarYa tengo lectura para las vacaciones de navidad :-)
¡Buen trabajo!